In the vein of ‘word problems can be a problem‘, I offer this worked solution to a trigonometry word problem that has stumped at least one student.
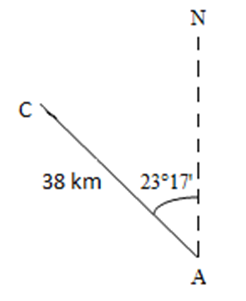
Chatham Island is located 38 kilometres N 23 degrees 17 minutes west of the community of Alert Bay. A boat in distress radios its position as N 17 degrees 35 minutes east of Chatham Island and N 18 degrees 41 minutes west of Victoria. How far is the boat from the city?
The first step is to make a drawing. We will use the letter C to represent Chatham Island, the letter A to represent Alert Bay and the letter N to represent due North.
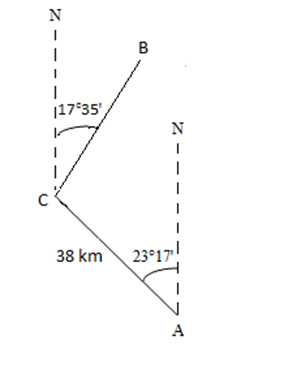
The boat is N 17 degrees 35 minutes of Chatham Island. We add it to the above drawing as B and get the following.
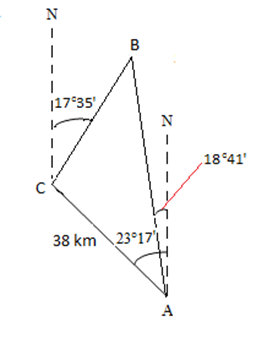
The boat’s position of N 19 degrees 41 minutes West of Alert Bay is the last bit of information we add.
So we can easily enter numbers into the calculator, we convert all angles to decimal degrees from degrees and minutes. We need to remember that one minute is one sixtieth of a degree or 1/60. So to convert the angle above Chatham Island we multiply the 35 minutes by 1/60 and then add that to the 17 degrees to get (rounded to the nearest ten thousandth) the following:
17.5833 degrees
Using the same approach with the other angles we get
18.6833 degrees
23.2833 degrees
Now that we have everything in the drawing, let’s take stock of what we know.
Side b (across from angle B) is 38 km. Therefore b = 38.
It is important to note that, at the moment we do NOT know what angle A, B or C are. In particular note that the angle at the bottom of the drawing, 23.2833 degrees, is NOT angle A. However, we can soon calculate angle A by subtracting
23.2833 degrees from 18.6833 degrees to get 4.6000 degrees. So now we know
A = 4.6000 degrees
How about the other angles? We can find angle C, if we apply some Intermediate Math geometry. Thanks to the two parallel lines, running due north, we can use the Transversal Postulate to determine angle C. See http://library.thinkquest.org/20991/geo/parallel.html for a more detailed description of this concept of parallel lines and congruent angles. See below for how we use this concept of congruent angles to determine angle C.
For simplicity, let’s remove line a (or AB) so we can focus on line AC and the two parallel lines.
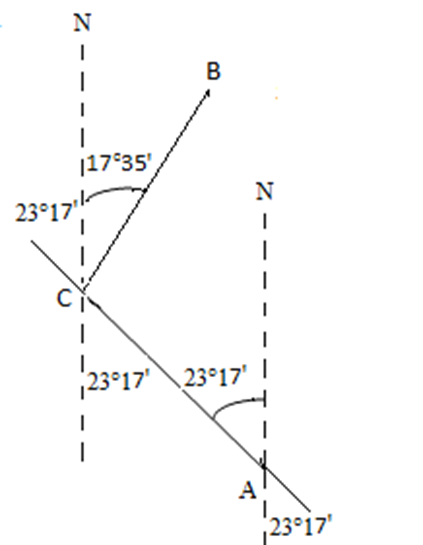
Now we add the given angle of 17.5833 to the determined angle of 23.2833 to get 40.8666 degrees.
17.5833 + 23.2833 = 40.8666
Remembering that a straight line has 180 degrees we can subtract 40.8666 from 180 degrees.
180 – 40.8666 = 139.1334
That tells us that angle C is 139.1334 degrees.
Also remembering that a triangle has 180 degrees, we can add angle A (4.6000 degrees) to angle C (139.1334 degrees) and then subtract that 180 degrees to find angle B.
180 – (4.6000 + 139.1334) = 36.2666
Thus angle B is 36.2666 degrees.
Let’s bring back the drawing of the original problem, now with all the angles included.
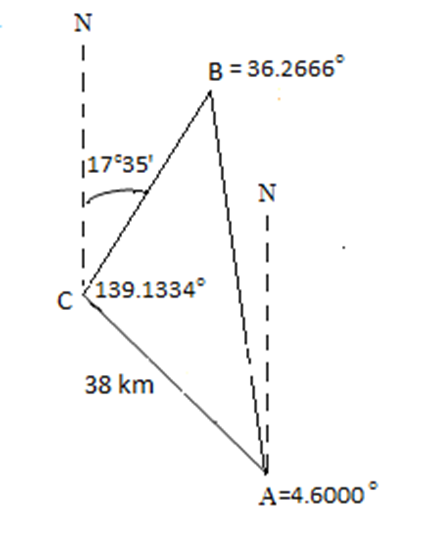
The distance the boat (B) is from Alert Bay (A) is represented by line BA (also known a line c). We use the law of sines to find c.
b/sin B = c/sin C
Substituting the appropriate values in, we have
38/sin 36.2666 = c/sin 139.1334
c = 38 x sin 139.1334/ sin 36.2666
c is approximately 42 km (rounded).
So the boat is 42 km from Alert Bay. Using the law of sins again we could also determine how far the boat is from Chatham Island.